Perpendicular from the Centre to a Chord

The perpendicular distance of a chord from the centre of a circle is $6 \mathrm{cm}$. If the length of the chord is $2 \mathrm{cm}$ less than thrice the perpendicular distance, what is the radius of the circle?

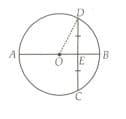
In the figure ,$O$ is the centre of the circle of radius $5 \mathrm{cm}$. $OP\perp AB, OQ\perp CD, AB\parallel CD, AB=6 \mathrm{cm}, CD=8 \mathrm{cm}$. Then $PQ$ is:

(Write the answer in $\mathrm{cm}$)

Find the length of a chord which is at a distance of $5 \mathrm{cm}$ from the centre of a circle of radius $13 \mathrm{cm}$. (Write the answer in $\mathrm{cm}$)

In the given figure, $\mathrm{CD}$ is the perpendicular bisector of the chord $\mathrm{AB}.$If $\mathrm{AB}=2 \mathrm{cm}, \mathrm{CD}=4 \mathrm{cm}$ and the radius of the circle is $r \mathrm{cm}$, then find the value of $r$ in decimal.

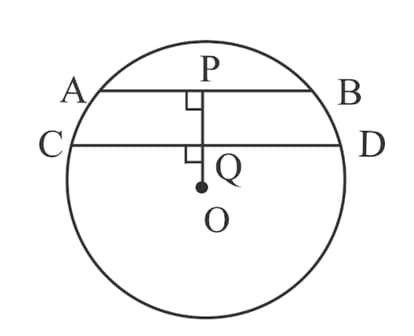
The length of the common chord of two intersecting circles is $30 \mathrm{cm}.$ If the radii of the two circles are $25 \mathrm{cm} \mathrm{and} 17 \mathrm{cm},$ find the distance between their centres.

The radii of two concentric circles are $17 \mathrm{cm} \mathrm{and} 10 \mathrm{cm},$ a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If $QR=12 \mathrm{cm},$ calculate PQ.

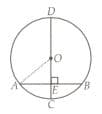
In given figure, CD is a diameter which meets the chord AB at E such that $AE=BE=4 \mathrm{cm}. \mathrm{If} CE=3 \mathrm{cm},$ find the radius of the circle.

An isosceles triangle $ABC$ with $AB=AC=25 \mathrm{cm} \mathrm{and} BC=14 \mathrm{cm}$ is inscribed in a circle. Calculate the radius of the circle. (Answer up to two places of decimal)

In a circle with diameter $10 \mathrm{cm},$ AB and CD are two parallel chords of lengths $8 \mathrm{cm} \mathrm{and} 6 \mathrm{cm}$ respectively. Calculate the distance between the chords if they are on the opposite sides of the centre.

In a circle with diameter $10 \mathrm{cm},$ AB and CD are two parallel chords of lengths $8 \mathrm{cm} \mathrm{and} 6 \mathrm{cm}$ respectively. Calculate the distance between the chords if they are on the same side of the centre.

In given figure, $AB$ and $AC$ are chords of a circle with centre $O$. IF $AB=24 \mathrm{cm}, AC =22 \mathrm{cm} \mathrm{and} OM=5 \mathrm{cm},$ find the value of $\mathrm{k}$, if $\mathrm{ON}=4\sqrt{\mathrm{k}} \mathrm{cm}$.

In a circle of radius $7.5 \mathrm{cm}$, $AB$ and $CD$ are two parallel chords of lengths $12 \mathrm{cm}$ and $9 \mathrm{cm}$ respectively. Calculate the distance between the chords, if they are on the opposite side of the centre.

In a circle of radius $7.5 \mathrm{cm}$, $AB$ and $CD$ are two parallel chords of lengths $12 \mathrm{cm}$ and $9 \mathrm{cm}$ respectively. Calculate the distance between the chords, if they are on the same side of the centre.

A chord of length $40 \mathrm{cm}$ is at a distance of $15 \mathrm{cm}$ from the centre of the circle. Calculate the radius of the circle.

Calculate the length of a chord of a circle of radius $13 \mathrm{cm},$ which is at a distance of $12 \mathrm{cm}$ from its centre.

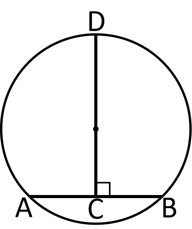
In the given figure, the diameter AB of a circle with centre O is perpendicular to the chord $PQ. \mathrm{If} PQ=8 \mathrm{cm} \mathrm{and} AM=2 \mathrm{cm},$ find the radius of the circle.

A chord of length $16$ cm is drawn in a circle of diameter $20$ cm. Calculate its distance from the centre of the circle.

Find the length of a chord of a circle which is at a distance of $8$ cm from the centre of the circle of radius $10$ cm.

In the given figure, $O$ is the centre of a circle and diameter $AB$ bisects the chord $CD$ at a point $E$ such that $CE=ED=8 \mathrm{cm}$ and $EB=4 \mathrm{cm}$. The radius of the circle is $r \mathrm{cm}$. The value of $\frac{r}{2}$ is

In the given figure, $CD$ is the diameter of a circle with centre $O$ and $CD$ is perpendicular to chord $AB$. If $AB=12 \mathrm{cm}$ and $CE=3 \mathrm{cm}$, then radius of the circle is $r \mathrm{cm}$. The value of $2r$ is